We begin by describing the simplest version of our model. Later on, we will introduce several modifications, in order to deal with time dependent parameters.
Consider a hidden process (the non-observable actual number of counts in the phenomenon under study) ![]() with Po-INAR(1) structure:
with Po-INAR(1) structure:
(1) ![]()
where ![]() is a fixed parameter,
is a fixed parameter, ![]() Poisson(
Poisson(![]() ), i.i.d., independent of
), i.i.d., independent of ![]() are the innovations, and
are the innovations, and ![]() is the binomial thinning operator:
is the binomial thinning operator: ![]() with
with ![]() i.i.d Bernoulli(
i.i.d Bernoulli(![]() ) random variables. Later on, we shall introduce time dependence, and hence we will be considering that
) random variables. Later on, we shall introduce time dependence, and hence we will be considering that ![]() is a funtion of
is a funtion of ![]() .
.
The INAR(1) process is a homogeneous Markov chain with transition probabilities
![Rendered by QuickLaTeX.com \[\mbox{\bf P}(X_n = i | X_{n-1} = j) = \sum_{k=0}^{i\wedge j} {j \choose k} \alpha^k (1-\alpha)^{j-k}\mbox{\bf P}(W_n=i-m)\]](https://underreported.cs.upc.edu/wp-content/ql-cache/quicklatex.com-b4c2c6ae57e5c5bf2b69a03a30a451d4_l3.png)
The expectation and variance of the binomial thinning operator are
![]()
![]()
A simple under-reporting scheme
The under-reported phenomenon is modeled by assuming that the observed counts are
(2) 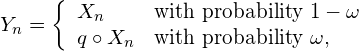
where ![]() and
and ![]() represent the frequency and intensity of the under-reporting process, respectively. We will eventually be interested in considering that
represent the frequency and intensity of the under-reporting process, respectively. We will eventually be interested in considering that ![]() is time dependent:
is time dependent: ![]() . That is, for each
. That is, for each ![]() , we observe
, we observe ![]() with probability
with probability ![]() , and a
, and a ![]() -thinning of
-thinning of ![]() with probability
with probability ![]() , independently of the past
, independently of the past ![]() .
.
Hence, what we observe (the reported counts) are
![Rendered by QuickLaTeX.com \[Y_n = (1- \mbox{\bf 1}_n)X_n + \mbox{\bf 1}_n \sum_{j=1}^{X_n} \xi_j \quad\quad \mbox{\bf 1}_n\sim\mbox{Bern}(\omega), \quad \xi_j\sim\mbox{Bern}(q)\]](https://underreported.cs.upc.edu/wp-content/ql-cache/quicklatex.com-05afc409dfd81fa407438967367fb14e_l3.png)
Properties of the model
The mean and the variance of a stationary INAR(1) process ![]() with Poisson(
with Poisson(![]() ) innovations are
) innovations are ![]() .
.
Its auto-covariance and auto-correlation functions are ![]() and
and ![]() respectively.
respectively.
Hence,
(3) ![]()
The auto-covariance function of the observed process ![]() is
is
![]()
Hence, the auto-correlation function of ![]() is a multiple of
is a multiple of ![]() :
:
![Rendered by QuickLaTeX.com \[\rho_Y(k)=\frac{(1-\alpha)(1-\omega(1-q))^2}{(1-\alpha)(1-\omega(1-q))+\lambda(\omega(1-\omega)(1-q)^2)}\alpha^{|k|}=c(\alpha,\lambda,\omega,q)\alpha^{|k|}.\]](https://underreported.cs.upc.edu/wp-content/ql-cache/quicklatex.com-e29d0096f34f8961001d4746695ae72d_l3.png)
Parameter estimation
The marginal probability distribution of ![]() is a \textbf{mixture of two Poisson distributions}
is a \textbf{mixture of two Poisson distributions}
(4) 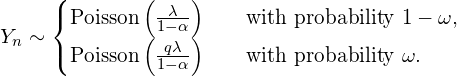
When ![]() the distribution of the observed process
the distribution of the observed process ![]() is a zero-inflated Poisson distribution.
is a zero-inflated Poisson distribution.
From the mixture we derive initial estimations for ![]() ,
, ![]() ,
, ![]() and
and ![]() , to be used in a maximum likelihood estimation procedure.
, to be used in a maximum likelihood estimation procedure.
The likelihood function of ![]() is quite cumbersome to compute,
is quite cumbersome to compute,
![]()
hence the forward algorithm (Lystig and Hughes (2002)), used in the context of HMC is a suitable option.
Consider the forward probabilities
(5) 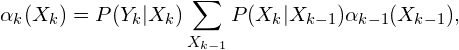
with ![]() .
.
Then, the likelihood function is
![]()
![]() and
and ![]() are the so-called emission and transition probabilities.
are the so-called emission and transition probabilities.
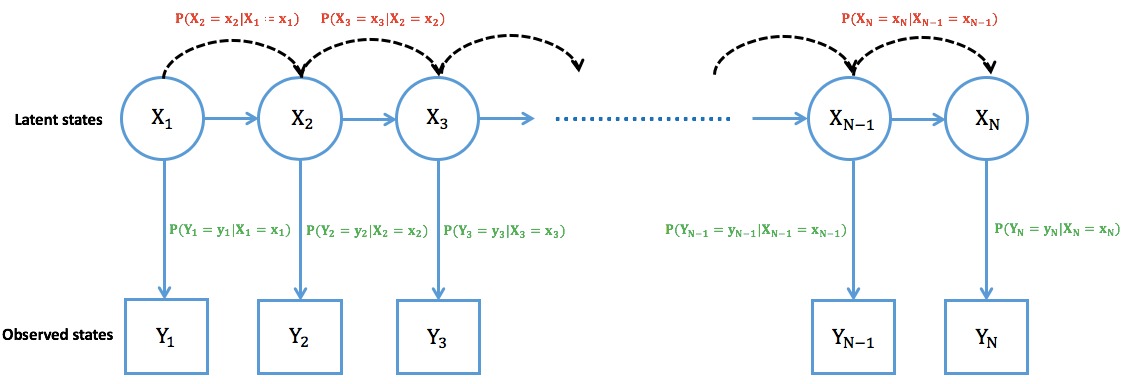
Transition probabilities are computed as
(6) 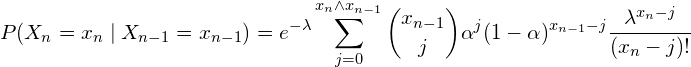
While emission probabilities are given by
(7) 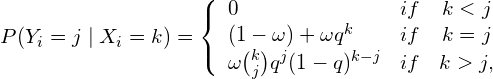
From this computations, a nonlinear optimization program computes the MLE estimates of the parameters.
Reconstructing the hidden chain ![]()
In order to reconstruct the hidden series ![]() , the Viterbi algorithm (Viterbi, 1967) is used.
, the Viterbi algorithm (Viterbi, 1967) is used.
The idea is to provide the latent chain ![]() that maximizes the likelyhood of the latent process given the observed series, assuming all the parameters are known.
that maximizes the likelyhood of the latent process given the observed series, assuming all the parameters are known.
Let ![]() be the likelihood function of the model, then
be the likelihood function of the model, then
![Rendered by QuickLaTeX.com \[P(X_{1:n}|Y_{1:n})=\frac{P(X_{1:n},Y_{1:n})}{P(Y_{1:n})}\]](https://underreported.cs.upc.edu/wp-content/ql-cache/quicklatex.com-6323e8ba0948fbd8f390821ea8791647_l3.png)
Since ![]() does not depend on
does not depend on ![]() , it is enough to maximise the probability
, it is enough to maximise the probability ![]() .
.
The hidden series is reconstructed as:
![]()
Predictions
Having observed ![]() , we are interested in predicting
, we are interested in predicting ![]() , for
, for ![]() , and in evaluating the uncertainty of these predictions.
, and in evaluating the uncertainty of these predictions.
From equation 3, we have that ![]() , so that, if we have a good estimate for
, so that, if we have a good estimate for ![]() , then we can predict
, then we can predict ![]() by means of its expectation
by means of its expectation ![]() .
.
From (1), assuming that the expectation of the innovations depends on ![]() , that is, the noise is Poisson(
, that is, the noise is Poisson(![]() ) it is straightforward to see that
) it is straightforward to see that
(8) 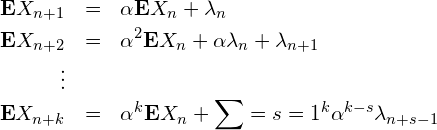
The easiest way to estimate ![]() is by substituting
is by substituting ![]() by
by ![]() in (3), to get
in (3), to get![]() , and then in 8 to get
, and then in 8 to get
(9) 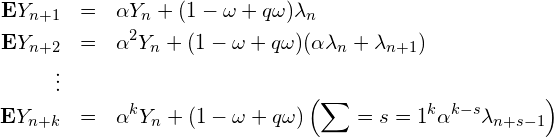
Bibliography
T.C. Lystig, J.P. Hughes (2002), Exact computation of the observed information matrix for hidden Markov models, Jr of Comp.and Graph. Stat.
Viterbi, A.J. (1967), Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory, 13, 260-269